Trie

对于给定前缀p要求返回集合中所有匹配该前缀的元素的一类问题，例如autocomplete和字典搜索，Trie是一个很自然的选择。

前两天闲的蛋疼，于是自己做了一个quick-and-dirty的实现，也算是小小地回顾了下当年造数据结构轮子的光景。

不考虑优化手段，trie的核心性质在于：给定一个字母表T， 每个trie node除了表示当前一个字符之外，还有len(T)个child nodes，每个child node对应下一个可能的字符，于是一个字符串就这样被保存在了路径上。

直觉上看，trie是通过增加宽度来减小高度（高度和最长的单词长度一直），以减小查询的时间复杂度。

不过在细节上，node保存的信息可以有不同处理：

第一种做法是node保存从root到此node的完整路径信息，如图：

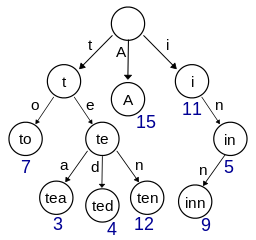
这么做的好处是之后需要路径信息时不需要额外的处理；当然不好的一点是node耗费的内存也变大了。

第二种做法是node仅保存当前字符的信息，如图：

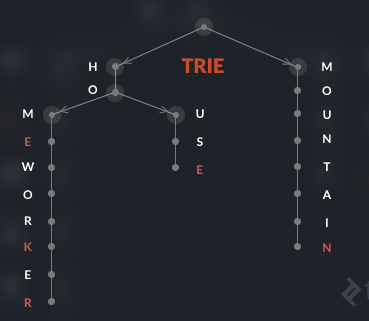
我最后选择了第二种做法。

另外，每个node还要有一个end-of-word的mark，因为路径中间的node有可能已经是一个完整的单词，例如he是here的前缀，但是两个都是完整的单词。

实现提供了三个接口：

  • Insert负责插入一个word到trie中
  • Contains检查trie当前是否存在某个word
  • Search接受一个前缀，返回一个包含所有满足改前缀的word的集合

接口的实现如果采用递归的话，会变成弱智一般的简单。

不过好在就算是采用迭代，也不会麻烦到哪里去，除了Search。

为了返回所有包含前缀的单词，实际上我们需要对trie做一个pre-order traversal，于是我们就有了一个stack。

一开始我是打算用stack保存一个node里还没有处理过的child nodes。这样就需要在迭代时不断往stack里加node，以及不断地从stack里取出node做处理。

我觉得这个思路很直接，并且觉着写起来会非常的流畅。但是有个不好的地方是，stack最多时需要保存所有的leaf nodes。而trie恰恰是通过增加宽度换取较低的高度，因此内存开销会比较大。

回龙观周杰伦大木老师提供了另外一个思路：利用stack保存正在处理的nodes。这样stack保存的恰好是构成目标字符串的路径，内存开销也成功压缩到了$O(h)$。

不愧是德艺双馨的亚洲人气小天王，服！

不过如果采用这个方法，还需要保存一个额外的信息，指明某个node已经处理过了多少child node，这样才能确定下一个要处理的child node。

别忘了一个node有字母表大小个children，而我们需要在node和他的child node之前来回切换。当然，如果语言自身提供了类似yield的设施，那实现就轻松多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
std::vector<std::string> Trie::Search(const std::string& prefix) const
{
    std::vector<std::string> words;

    // Locate the node matching the last character of `prefix`.
    const TrieNode* node = header_;
    for (char ch : prefix) {
        auto pos = Alphabet::GetCharacterIndex(ch);
        if (pos == Alphabet::npos) {
            return words;
        }

        const TrieNode* child = node->children[pos];
        if (!child) {
            return words;
        }

        node = child;
    }

    // We use `processing_nodes` as a stack to maintain nodes that are being processed.
    using CludeNode = std::pair<const TrieNode*, size_t>;
    std::vector<CludeNode> processing_nodes;
    processing_nodes.emplace_back(CludeNode(node, 0U));
    while (!processing_nodes.empty()) {
        // Don't access `current` after having pushed another node into `processing_nodes`.
        // Because the push might result in memory reallocation, rendering `current` an invalid
        // reference.
        auto& current = processing_nodes.back();
        bool child_node_found = false;
        while (current.second < current.first->children.size()) {
            const TrieNode* child = current.first->children[current.second];
            ++current.second;
            if (child) {
                processing_nodes.emplace_back(CludeNode(child, 0U));
                child_node_found = true;
                break;
            }
        }

        if (!child_node_found) {
            if (processing_nodes.back().first->last_char_of_word) {
                std::string word = prefix;
                std::for_each(processing_nodes.cbegin() + 1, processing_nodes.cend(),
                              [&word](const auto& clude_node) {
                    word += clude_node.first->character;
                });
                words.push_back(std::move(word));
            }

            processing_nodes.pop_back();
        }
    }

    return words;
}

对于写迭代形式的算法，我一直比较推荐采用循环不变式（loop invariant）去理解的做法。这几乎是我认为一个人能从算法导论里学到的最精华的基础。

Ternary Search Tree

默认的trie内存开销比较大，所以又有很多针对内存做了优化的改进数据结构，ternary search tree便是其中之一。

如名所述，ternary search tree的一个node只有三个child nodes：left, middle, right。

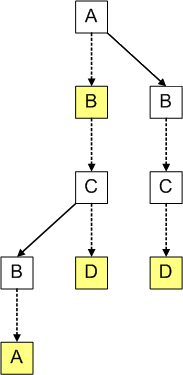
三子节点的做法来源于，一次比较会产生三种结果：大、小、相等。

假设字符间的大小关系为字符在字母表的先后顺序，TST的核心规则如下：

  • 如果字符c和当前node的字符相等，表示当前字符匹配，则进入当前node的middle-child
  • 如果字符c比当前node的字符小，则进入当前node的left-child尝试匹配
  • 如果字符c比当前node的字符大，则进入当前node的right-child尝试匹配

如果把TST放在一个三维空间上考虑的话，我认为left-child和right-child更像是当前node的sibling nodes。

匹配过程就像从顶部的root node一直向下搜索，匹配时middle-node连接下一层的node，失败时在当前层由sibling nodes构成的平面上搜索。

不过因为二维平面更加容易理解，所以还是在这个维度上考虑。

Insert和Contains的非递归实现并不难，只要选择好loop invariant。

我在实现时选择的loop invariant是：

  1. 每次对一个字符的迭代结束后，一定停留在这个字符对应的node上
  2. 每次开始迭代时，始终尝试进入当前node（上一轮迭代结束停留的位置）的middle-node
  3. 第2步失败时，根据比较信息在左子树/右子树中找到目标node

并且为了实现方便，root node被我实现为一个sentinel node。

不过非递归的Search实现起来非常繁琐，因为一个node的三个child nodes不在一个语义层，所以需要为了遍历需要用两个stack维护不同的信息。

我在纸上尝试了一下就回头选择了递归地实现=’’=。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
void SearchWord(Node* node, std::vector<std::string>* words, std::vector<char>* seq,
                const std::string& prefix)
{
    seq->push_back(Alphabet::GetCharacter(node->char_index));
    if (node->end_word) {
        std::string word(prefix);
        word.append(seq->begin(), seq->end());
        words->push_back(std::move(word));
    }

    if (node->children[Node::kMiddle]) {
        SearchWord(node->children[Node::kMiddle], words, seq, prefix);
    }

    seq->pop_back();

    if (node->children[Node::kLeft]) {
        SearchWord(node->children[Node::kLeft], words, seq, prefix);
    }

    if (node->children[Node::kRight]) {
        SearchWord(node->children[Node::kRight], words, seq, prefix);
    }
}

std::vector<std::string> TernaryTree::Search(const std::string& prefix) const
{
    std::vector<std::string> words;

    // Locate the node matching the last character of `prefix`.
    const Node* node = root_;
    for (char ch : prefix) {
        auto index = Alphabet::GetCharacterIndex(ch);
        if (index == Alphabet::npos) {
            return words;
        }

        const Node* next_node = node->children[Node::kMiddle];
        if (!next_node) {
            return words;
        }

        while (index != next_node->char_index) {
            if (index < next_node->char_index) {
                next_node = next_node->children[Node::kLeft];
            } else {
                next_node = next_node->children[Node::kRight];
            }

            if (!next_node) {
                return words;
            }
        }

        node = next_node;
    }

    if (node->end_word) {
        words.push_back(prefix);
    }

    std::vector<char> sequence;
    if (node->children[Node::kMiddle]) {
        SearchWord(node->children[Node::kMiddle], &words, &sequence, prefix);
    }

    return words;
}

完整的实现在这里

Epilogue

我会写Trie是因为看到了the-trie-a-neglected-data-structure这篇文章，有张图片也是从文章里截取的。

而Ternary Search Tree则是不小心看到了efficient-auto-complete-with-a-ternary-search-tree，同样从文章里“借”了一张图片

再次对两位作者表示感谢！

其实一开始写实现时，我犹豫了一会儿是应该用raw pointer还是smart pointer。虽然raw pointer不是什么evil的东西，但是owned raw pointers对我来说始终有点不太舒服。

后来我看见了这个post，再联想C++提供的muli-paradigms的目的就是为了offer you the best-practice whenever you need, and you don’t pay what you don’t use。

于是我就不断地给自己洗脑：nodes themselves are resources managed by a Tree.

再然后，我就释然了XD。