离职前夕清理公司硬盘数据的时候，偶然发现原来自己去年三月份的时候还写过一个 non-intrusive buddy allocator 呢。因为时间太过久远加上之前写的时候没有加上该有的注释，导致花了一番功夫才看懂核心算法再写什么，更别说几个看起来完全不明觉厉的 offset-to-address 的计算。

于是我想，应该有必要整理一下，万一哪天真的需要呢？

Theory

Non-intrusive 的做法是，不在实际分配的内存中加入 meta-data，而是将 buddy-allocator 自身做成一个 allocation bookkeeper。

考虑到 allocator 要求管理的内存块必须是$2^k, k \in Z$大小，我们可以把一块内存对应的 bookkeeping 做成一棵 perfect binary tree。以大小为 8K 的内存块为例，对应的 perfect binary tree 结构如下：

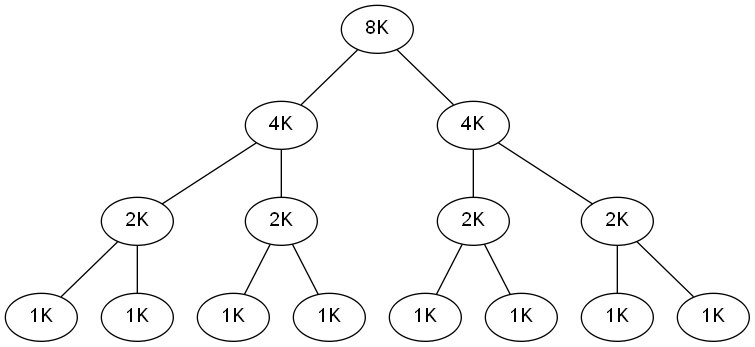
每一个节点对应内存块中的一个可用区域（考虑从上往下的映射）；最下层叶子节点对应完整的内存块，每个叶子节点对应一个最小的内存单元；父节点对应的内存区域包含子节点对应的内存区域。

而 perfect binary tree 又可以用数组来表示（实际上是特殊的 complete binary tree），一方面可以提升内存利用率（没有额外的前后继指针），又可以提高访问性能（减少动态分配以及连续内存带来的 cache-locality）。

Implementation

为了实现方便以及让分配、释放算法看起来更加简洁，作如下两个设定

  • 定义 maximum consecutive block (MCB) 为一个能被直接管理的最大的连续内存区域，大小仍然要满足$2^k$的要求
  • 用 bookkeeper tree 中的每个节点去保存对应内存区域的 MCB 的大小

于是得到对于每一个节点的递归定义

$$M(i)=\begin{cases}\max\left\{M(LC(i)),M(RC(i))\right\} & \text{otherwise}\\M(LC(i))+M(RC(i)) & M(LC(i))=M(RC(i))\end{cases}$$

上面 $M(i)$ 表示节点 $i$ 的 MCB 值，也即实际保存在节点里的值；$LC(i)$ 和 $RC(i)$ 分别表示节点 $i$ 的左子节点和右子节点。

仍然以前面 8K 大小的内存块举例，假设我们要从内存块里分配出大小 1K 的内存，那么这棵树的状态则变成如下样子：

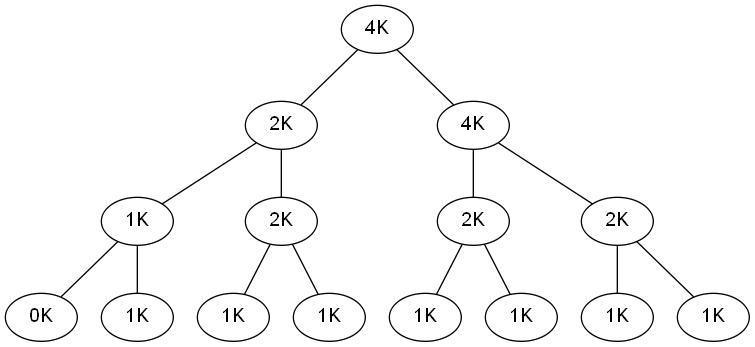
后面实现过程中会发现这个定义解决掉了很多麻烦。

implementing allocation

分配算法大体顺序如下：

  1. 比较请求分配的内存大小和根节点的值，确认是否还有足够的空间可以分配。如果根节点的大小小于请求大小，很明显没有空间了。
  2. 如果空间足够，则沿着根节点向下搜索，采用 last-fit strategy，即最后一个满足要求的节点，找到目标节点。因为父节点覆盖的内存区域是包括子节点的，所以要使用 last-fit。
    实际上我们可以利用一个性质来简化第2步的逻辑：如果存在满足要求的节点，那么具有这个大小的节点所在的 depth/height 是固定的，和树当前状态无关（得益于前面 MCB 的定义）。于是我们可以在一棵假想的、全新的树上遍历，结合实际的树的信息去判断左右的走向。
  3. 将目标节点标记为0，然后回溯向上到根节点，修正路径上节点的信息。
  4. 假设目标节点在数组中的序号为 $i$，那么利用公式 $\text{offset} = (i+1) \cdot \text{block_size_needed} - \text{total_block_size}$ 算出分配的内存的起始序号相对于完整内存块的偏移量（其实就是内存块对应的第一个叶子节点在整个叶子节点中的序号）。
    至于这个公式怎么来的，后面再说。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
size_t BinManager::Allocate(size_t slots_required)
{
    assert(slots_required != 0);
    if (slots_required == 0) {
        return noffset;
    }

    size_t slots_needed = buddy_util::NearestUpperPowerOf2(slots_required);
    if (max_consecutive_slot_[0] < slots_needed) {
        return noffset;
    }

    size_t index = 0;
    for (auto node_slots = total_slot_count_;
        node_slots != slots_needed;
        node_slots >>= 1) {
        if (max_consecutive_slot_[buddy_util::LeftChild(index)] >= slots_needed) {
            index = buddy_util::LeftChild(index);
        } else {
            index = buddy_util::RightChild(index);
        }
    }

    // The relative distance from first slot in the bin just now allocated to the
    // first slot in the underlying raw memory chunk.
    size_t offset = (index + 1) * slots_needed - total_slot_count_;

    max_consecutive_slot_[index] = 0;
    while (index) {
        index = buddy_util::Parent(index);
        max_consecutive_slot_[index] = std::max(
            max_consecutive_slot_[buddy_util::LeftChild(index)],
            max_consecutive_slot_[buddy_util::RightChild(index)]);
    }

    return offset;
}

Deallocation

释放的过程就相对简单。

输入是前面 allocation 过程得到的 offset，首先转换利用上面的公式的变形（上面公式中的 block_size_needed 等于叶子节点的大小，为1），转换得到原来的 $i$，然后从 $i$ 指向的叶子节点开始，向上搜索，碰到的第一个标记为0的节点就是要找的目标节点，恢复其大小（前面提到的性质）。

接着仍然向上回溯到根节点，修正路径上的节点信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void BinManager::Free(size_t offset)
{
    // The value of noffset can be regarded as positive infinity.
    assert(offset < total_slot_count_);
    if (offset >= total_slot_count_) {
        return;
    }

    // Since multiple indices can be mapped into a single offset, we backtrace to
    // locate the bin from bottom.
    // The first bin we meet in the path whose slot count is 0 is the target.
    // Incorrect |offset| may cause undesired deallocation for yet another bin.
    size_t node_slot_count = 1;
    size_t index = offset + total_slot_count_ - 1;
    while (max_consecutive_slot_[index]) {
        // Reached the root. The |offset| is incorret.
        if (index == 0) {
            return;
        }

        node_slot_count <<= 1;
        index = buddy_util::Parent(index);
    }

    max_consecutive_slot_[index] = node_slot_count;
    while (index != 0) {
        index = buddy_util::Parent(index);
        node_slot_count <<= 1;

        size_t lc_slots = max_consecutive_slot_[buddy_util::LeftChild(index)];
        size_t rc_slots = max_consecutive_slot_[buddy_util::RightChild(index)];

        // Merge adjacent bins if possible.
        if (lc_slots + rc_slots == node_slot_count) {
            max_consecutive_slot_[index] = node_slot_count;
        } else {
            max_consecutive_slot_[index] = std::max(lc_slots, rc_slots);
        }
    }
}

Derivation of the Formula

最后解释一下怎么得到公式 $\text{offset} = (i+1) \cdot \text{block_size_needed} - \text{total_block_size}$。

首先做如下假设

  • 拥有的总内存块 total_block_size 为 $2^n$
  • 请求的内存大小 block_size_needed 是 $2^k$
  • 目标节点在数组中的序号是 $j$
  • perfect binary tree 对应的数组下标从1开始，i.e. 根节点在数组中的序号是1。这个假设是必要的，因为可以让左右子节点的公式更加简单

基于上述假设，我们就有

  1. 目标节点所在的高度一定是 $k$ （叶子节点位于高度0）。于是目标节点覆盖的第一个子节点的序号是 $j \cdot 2^k$。只需要不断的访问左子节点，直到叶子
  2. 第一个叶子节点的序号是 $ 2^n $
  3. 算得两个叶子节点的偏移量 $ \text{offset} = j \cdot 2^k - 2^n $
  4. 因为实现时数组下标 $i$ 从0开始，所以我们有 $ j = i + 1$
  5. 带入(3)中的式子，得到 $\text{offset} = (i+1) \cdot 2^k - 2^n $

公式就这样出来了，基本没有什么太复杂的东西。

假设数组从1开始也是一个常用的技巧，可以极大地简化运算和推导。所以你会看到算法导论里的数组一直都是从1开始的，因为是在可以极大的简化分析。而最后也只需要一个线性变换就拿到了实际环境下的公式。

安利时刻

对于非侵入式的 allocator 来说，前面实现的分配/释放只起到了 bookkeeping 的作用。你还需要自己提供一个能够分配/释放真实内存的模块，并利用前面实现的 buddy allocator 去管理。

一个完整的实现可以参考这里。

这个实现里核心的部分是

  • MemoryBin：提供真实、连续的内存块，由一个个 slot 组成，每个 slot 大小可以设置，默认是 4KB
  • BinManager：基于 buddy allocator 的 bookkeeper，管理的基本单位是 MemoryBin 中的 slot
  • BuddyAllocator：前两个类的一个 facade，透露给外部用户的接口层